迅速判讀試驗序列分析(Trial Sequential Analysis, TSA)

 

2022 年底新學會的統計方法，簡單做了整理，方便日後複習，也希望對大家有幫助～

傳統統合分析可能有偽陽性存在

傳統統合分析的好處是，可以將同一主題多篇的隨機對照試驗（Randomized, controlled trial, RCT）合併起來，增加樣本數來提高對結果的精確度（信心程度）；然而，當研究篇數或樣本數尚不充足的時候，合併出來的結果是很容易浮動的，可能 2021 年統合分析結果有顯著性療效，一年後，新的 RCT 發表，2022 年的統合分析結果卻是不顯著。此時，2021 年的顯著結果可能就是偽陽性了（實際上沒效，但研究做出來有效）。

TSA 圖中的新玩意

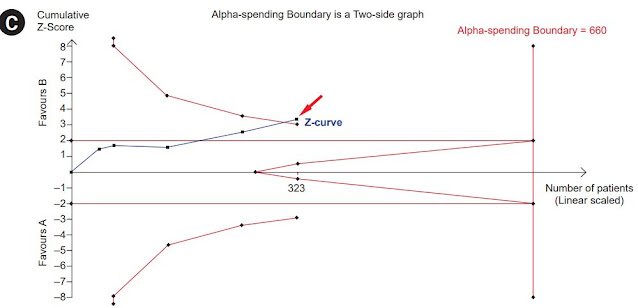
試驗序列分析(Trial Sequential Analysis, TSA) 呈現的圖中，除了傳統邊界（Conventional Boundary）外，還多了 TSA 邊界（TSA Monitoring Boundary）以及無效邊界（Futility Boundary）。 Z-curve 呈現所有研究逐步累加的過程，每一點代表一個研究，最後一點即統合分析的結果。

TSA 提高｢差異｣的閾值，降低偽陽性風險

TSA 邊界比傳統邊界來得嚴格，這樣的差異會隨著研究數、樣本數增加而趨近。

Z-curve 最後一點穿越傳統邊界後，可得傳統的顯著差異結論。但若 Z-curve 已經大到足以穿越 TSA 邊界，我們幾乎有足夠的信心指出該效果量為真，而非偶然所見的偽陽性。

TSA 的無效邊界更加強了無效的結論

結果尚不明朗時，會有越來越多研究執行，有的結論有效，有的無效；但當統合的總結果已經趨近無效時，急需一個足夠有信心的結論證明｢真的沒效｣，才能避免人力、金錢及資源的浪費（做人體研究真的很燒錢啊！）。無效的結果以 TSA 圖呈現，Z-curve 連傳統邊界都無法穿越，更別說超越 TSA 邊界了！既然沒有足夠信心指出有效性，那有沒有辦法指出其｢無效性｣？

｢無效邊界｣內的三角區域給出了明確的範圍，只要 Z-curve 最終落於此處，就有足夠信心指出結果無效。

圖解說明

↑ Z-curve 超出傳統邊界，有傳統的統計顯著，但沒有超出 TSA 邊界，因此可能有偽陽性

↑ Z-curve 未超出傳統邊界，但也未落於無效邊界，因此需要更多研究，才知道有效還無效

↑ Z-curve 超出傳統邊界，也超出 TSA 邊界，有足夠信心指出結果有效

↑Z-curve 未超出傳統邊界，但落於無效邊界，有足夠信心指出結果無效

其他還有 Interim analysis, O'Brien-Fleming's method, Optimal information size 也是 TSA 統計方法中很重要的觀念，有時間的話再來補更新囉 QQ

Reference

1. De Cassai A, Pasin L, Boscolo A, Salvagno M, Navalesi P. Trial sequential analysis: plain and simple. Korean journal of anesthesiology. 2020 Dec 18;74(4):363-5.
2. Kang H. Trial sequential analysis: novel approach for meta-analysis. Anesthesia and Pain Medicine. 2021 Apr 30;16(2):138-50.
3. Roshanov PS, Dennis BB, Pasic N, Garg AX, Walsh M. When is a meta-analysis conclusive? A guide to trial sequential analysis with an example of remote ischemic preconditioning for renoprotection in patients undergoing cardiac surgery. Nephrology Dialysis Transplantation. 2017 Apr 1;32(suppl_2):ii23-30.
4. Wetterslev J, Jakobsen JC, Gluud C. Trial sequential analysis in systematic reviews with meta-analysis. BMC medical research methodology. 2017 Dec;17(1):1-8.